HOG (Histogram 直方图 of Oriented 朝向 Gradients 梯度 渐变)

梯度：在图像处理中，梯度可以理解为图像亮度变化的方向和大小。如果一个像素点的亮度突然变化，那么这里就可能存在一个边缘。

方向：梯度不仅有大小，还有方向。比如，一个边缘可能是水平的，也可能是垂直的，或者斜着的。

step1：卷积求梯度

# 假设一个图片是这样
img = np.array([
    [150, 160, 170, 150, 160, 170],
    [180, 190, 200, 180, 190, 200],
    [210, 220, 230, 210, 220, 230],
    [180, 190, 200, 180, 190, 200],
    [210, 220, 230, 180, 190, 200],
    [210, 220, 230, 180, 190, 200]
])
x_kernel = [-1,0,1]
y_kernel = [-1,0,1]
# 1.开始卷积(0,0)坐标
# x方向
# -1 0 1 对应 [0,150,160] 通过ai得知hog对于边界处理方式是忽略，因此(-1,0)坐标值设置为0
# 卷积得到值为 160 那么(0,0)的Gx为160

# y方向
# -1 0 1 0 150 180 卷积得 180 (0,0)的Gy为180
# 根据下面梯度公式计算梯度大小和方向得
# 梯度方向 = 48.37°
# 梯度大小 = 240.83

注：从左往右第一个50为Gx第二个50为Gy，从上往下第一个50为Gy第二个50为Gx

step2：加权

将180°分为9份（默认为9），从0开始步进为6，分别为0，20，40，60，80，100，120，140，160。将梯度方向对应的角度分别对应，如果相对应则将梯度大小分配在上面

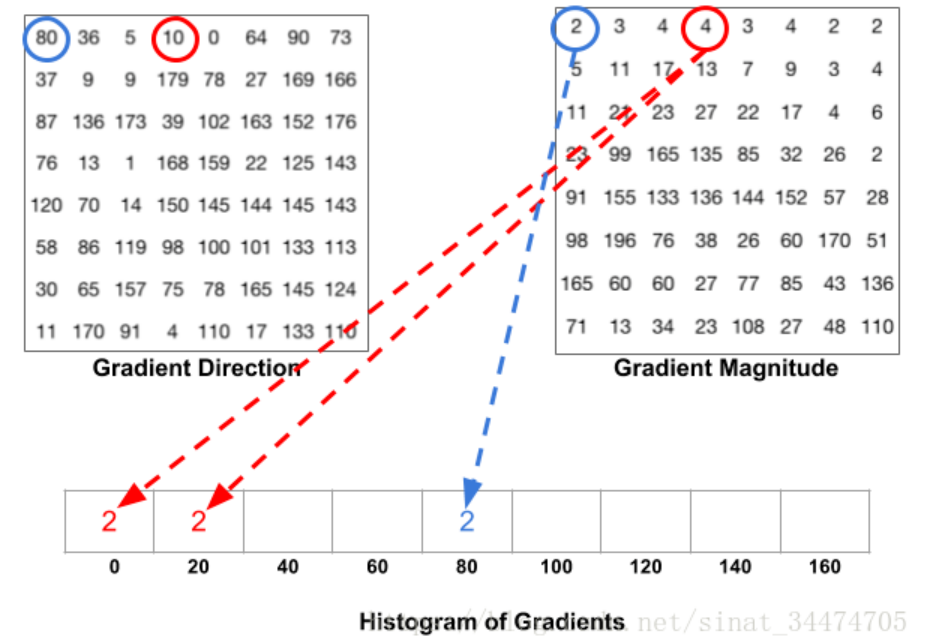
让我们看下面的图：

大小为60，角度为25，我们要分别计算20和40的bin分布的值使用公式：

左bin分布值 = 右bin值 - 梯度角度 / (右bin值 - 左bin值) * 梯度大小

右bin分布值 = 梯度角度 - 左bin值 / (右bin值 - 左bin值) * 梯度大小

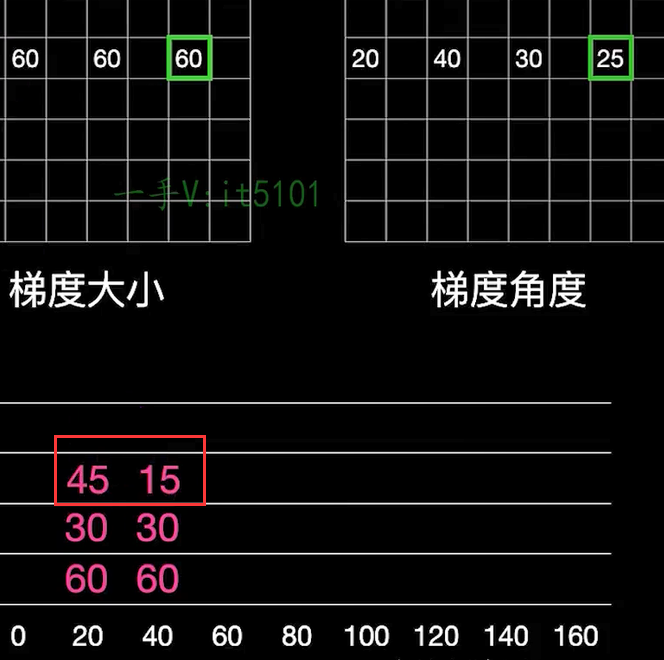
如果值 >160则分别分布在160和0 bin上

这样每8*8的像素就获得了9个bin称之为cell

step3：归一化

我们使每2*2个cell为一个block，将这个block中的bin平方累加再开根号即可得到一个平均值，再分别用bin值去除以这个平均值即可得到标准化向量。

比如一个RGB颜色向量为[128, 64, 32]。这个向量的长度是

$$ √128^2+64^2+32^2=146.64 $$

这也叫做向量的L2范数。

归一化的目的是为了防止光照及噪点等对识别产生的影响

step4：拼接所有向量

每个块有4个cell，一个cell有9个bin，那么一个block就有4*9=36个特征向量，假设图片的宽高分别为64*128，卷积核为8*8

那么我们一共有：

(64-8)/8=7个水平block
(128-8)/8=15个垂直block

由此可知这个图片一共有7*15*36=3780个维度向量

我们将所有向量拼接返回就得到了图片的特征向量

作者的话

最后一步拼接似乎就是skimage.feature.hog返回的特征向量，但是否一样我没有尝试，有知道的朋友还请评论告知，感谢